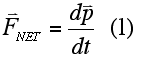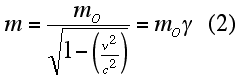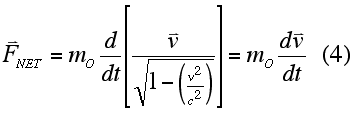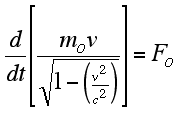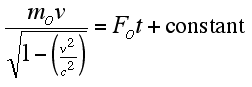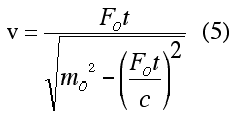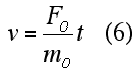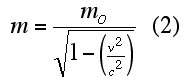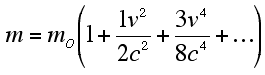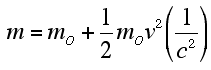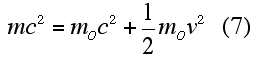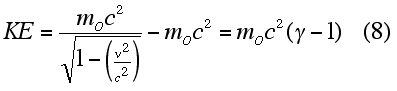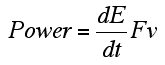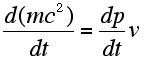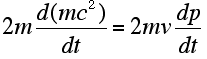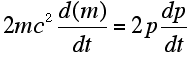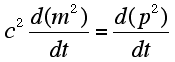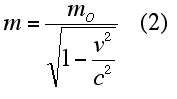Mass, Inertia, & Newton's 2nd Law:
| In order for all of the laws of physics to "work" in all inertial frames of reference (Einstein's 2nd Postulate of Special Relativity), it is necessary to modify our formulation for mass. Why is this so? |
Using the Lorentz transformation we previously derived, it follows that the acceleration of an object is not the same in different inertial frames of reference. Therefore, if Newton's Second Law (FNET = ma) is correct in one inertial frame, it will not be in another. The most important aspect of force is given by Newton's Third law, from which it can be shown that the momentum of an isolated system is conserved. Consequently, Einstein found it necessary to modify Newton's Second Law so that it satisfied his second postulate and correctly predicted the conservation of momentum for an isolated system.
| At the suggestion of Max Planck, Einstein modified Newton's Second Law by starting with an alternate formulation, namely: |
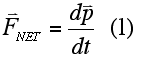 |
| Without going into the proof here, Einstein found that in order to satisfy his second postulate and conserve momentum in an isolated system, the mass of a particle must depend upon its speed, v. The relationship he derived is to the right, where mo is the object's "rest mass." |
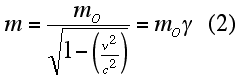 |
Therefore:
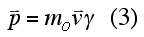
or
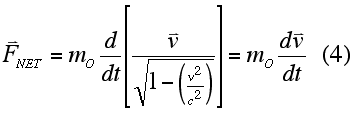
What is this saying? Classically, Newtonian physics says that if we apply a constant force to an object, the velocity of the object will increase uniformly (constant acceleration). If we maintain that force for a long enough period of time, then the object will eventually achieve a speed greater that c. Relativistically, this is not possible. The Lorentz transformation for the speed of an object in a moving, inertial frame cannot exceed c when viewed from a second, stationary inertial frame. Consequently, in relativistic terms, if we apply a constant force to an object, it is the momentum that increases uniformly. At speed approaching c, there is practically no acceleration as there is little change in v. The increase in momentum is accounted for by an increase in the object's "inertial" mass, m.
| If we consider an object with a rest mass, mo, initially at rest at the origin of a particular reference frame and apply a constant force, Fo, in the x-direction (for the sake of simplicity), the object's velocity (as a function of time) can be found as follows. In this case, Eq. 4 becomes the equation to the right, where v is the velocity along the x-axis. |
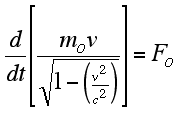 |
| The indefinite integral (or anti-derivative) of this relationship is: |
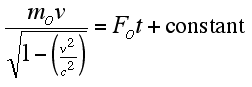 |
| Since v = 0 at t = 0, the constant is therefore zero. Solving algebraically for v |
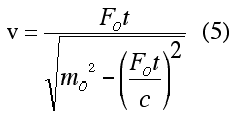 |
| Note that for v<<c, this relationship simplifies to the equation on the right, which is the relationship expected from Newtonian mechanics. However, in the case of the Newtonian result, the speed can increase without limit whereas with the relativistic formulation, the speed of the object cannot exceed c. |
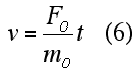 |
The Connection Between Relativistic Mass and Energy:
| Starting with the formulation for relativistic mass |
we can use the binomial theorem to expand this relationship as follows
|
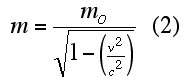
|
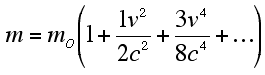
|
| For v<<c, this relationship can be given as |
Multiplying through by c^2, one obtains
|
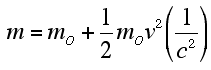
|
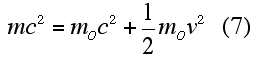
|
Note that the (1/2)mov^2 term represents the kinetic energy of an object with rest mass, mo. The other two terms, moc^2 and moc^2, represent the object's "rest energy" and total energy respectively.
| Therefore, relativistically the kinetic energy of an object is given by |
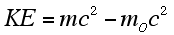
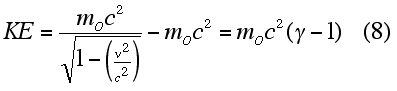
|
Another Way of Looking at Energy and Mass:
|
Starting from the definition of power
|
Multiplying through by 2m,
|
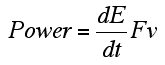
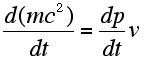
|
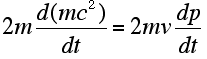
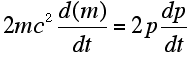
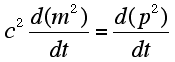
|
Taking the indefinite integral (anti-derivative)
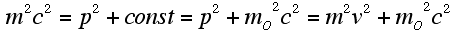
|
Solving this relationship for v, one finds:
|
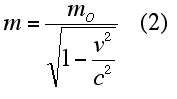
|
|
|
Text versions of the equation work are made with Microsoft Equation Editor and are embedded in Microsoft Word documents.
|
|
|