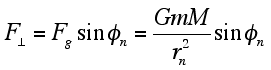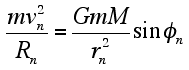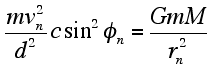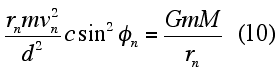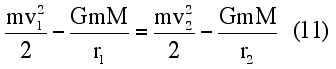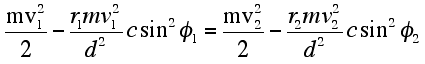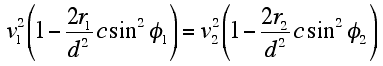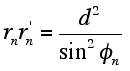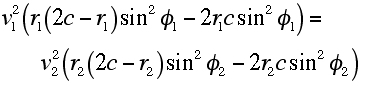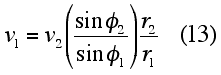|
|
 |
|
In teaching Introductory College or University Physics to undergraduates or advanced high school students, problems involving elliptical orbits are frequently presented with the objective of enriching the students’ understanding of orbital mechanics. An exercise nearly always encountered in these first-year classes consists of relating the velocity of a satellite (whose mass is treated as being insignificant compared to that of the central body) at its apoap-sis to the velocity of the satellite at its periapsis.1,2
The teacher is able to assure the students that the relationships are equivalent (both physical laws must hold), though it is by no means obvious that this is so by inspection alone. The following derivation uses Newton’s Law of Universal Gravitation in conjunction with centripetal force and elliptical geometry to construct the simple relationship so easily produced by the law of conservation of angular momentum. The equivalency of the two results is then apparent. The apoapsis/periapsis presentation (Part I) is suitable for most high-school AP-type classes and non-calculus college courses, although many students in those classes are unfamiliar with the elliptical geometry involved and must either take those results on faith or work through the geometric proofs as well. A more general presentation of the equivalence of the two methods (Part II) integrates well into calculus-based University Physics courses.
Part I: Velocities at Apoapsis and Periapsis
At the apoapsis of the orbit (see Fig. 1), the centripetal force is supplied by gravity
where RA, the radius of curvature of the ellipse,3 is given by the relationship
since phi, the angle between the radius vector and the tangent to the ellipse (see Fig. 2), is 90 degrees at apoapsis and periapsis. Substituting for the radius of curvature in Eq. (3),
For an ellipse, Substituting these relationships into Eq. (5),
Similarly, at periapsis, it follows that Eqs. (6a) and (6b) state the magnitude of the potential energy deficit of the satellite at apoapsis and periapsis in terms of its kinetic energy and the extremes of the orbital radii. This result could be obtained directly from the expression for the total energy of a satellite in elliptical orbit derived from the conservation of energy and angular momentum laws. The point to emphasize to students is that this derivation does not rely on the conservation of angular momentum per se, but on centripetal force and elliptical geometry.
Substituting Eqs. (6a) and (6b) into Eq. (7), one is left with
This relationship reduces to the result determined by the application of the conservation of angular momentum (Eq. 1) in the following manner
Part II: General Relationship of Velocities at All Points on an Elliptical Orbit
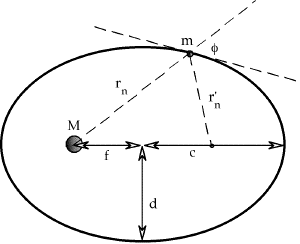
Fig. 2. General geometry of an elliptical orbit. In general, the angular momentum of a satellite in earth orbit is
which in its scalar form is
Consequently, by the conservation of angular momentum, the speed (v1) of the satellite at a particular point in its elliptical orbit can be found by knowing its speed, v2, at another point in its orbit in the following way:
Fig. 3. Geometry of velocity and force vectors of an elliptical orbit. It is this component of the force of gravity that supplies the perpendicular (centripetal) acceleration to the satellite. Therefore,
Substituting in for the radius of curvature, Rn (Eq. 4), and simplifying, one obtains the following general relationship (Eq. 10).
By the conservation of energy, Making the appropriate substitutions of Eq. (10) into Eq. (11), one obtains:
From the geometry of an ellipse3 , it is known that
Using these expressions in conjunction with Eq. (12),
References
|
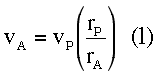
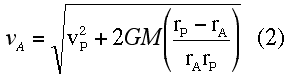
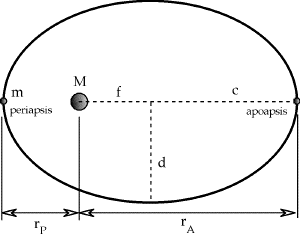 Fig. 1. Geometry of an elliptical orbit at apoapsis and periapsis.
Fig. 1. Geometry of an elliptical orbit at apoapsis and periapsis.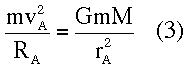
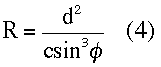
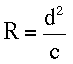
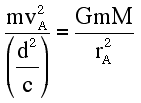
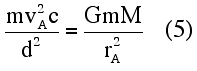
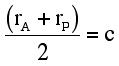 and it can be shown that
and it can be shown that 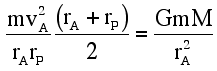
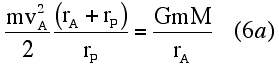
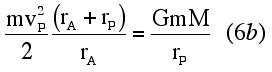
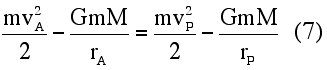
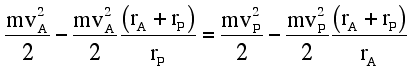
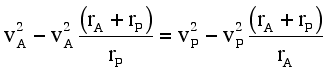
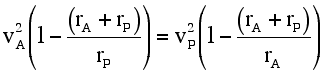
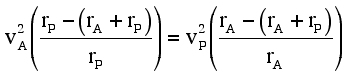
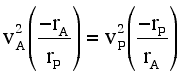
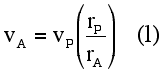
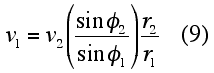
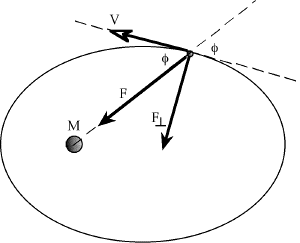 In order to demonstrate the general equivalence of this method to the conservation of energy method, we begin by considering the perpendicular component of the force of gravity, , acting on the satellite (see Fig. 3).
In order to demonstrate the general equivalence of this method to the conservation of energy method, we begin by considering the perpendicular component of the force of gravity, , acting on the satellite (see Fig. 3).