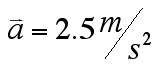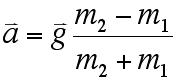 |
|
|
The Problem: Find a General Solution for the Simple Atwood Machine  An Atwood Machine is a simple device consisting of an ideal pulley and two masses connected over the pulley by an ideal string (see diagram at right). The problem is to find the acceleration of the system and the tension in the connecting string given the two masses. The problem will first be solved numerically with masses of 3 kg and 5 kg, then a general solution will be developed.Try the solution yourself--there are several approaches that will work. You can apply Newton's Second Law to each mass individually, you can apply Newton's Second Law to the system as a whole (solving for acceleration only), or you can use an energy-based technique (solving for acceleration only). Before viewing our solution, think about what values you would expect for the acceleration and for the tension of the string. What would a good guess for the acceleration be? What would a good guess for the tension be? What should happen to the acceleration as the values of the masses become more unbalanced?
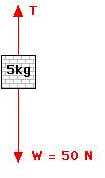
A General Solution for the Simple Atwood Machine: Conceptual ideas– The acceleration should be somewhat less than one "g" ("g" is approximately 10 m/s^2). As the masses become more unbalanced, the acceleration should approach one "g". If the masses are even, the acceleration is zero (they are in equilibrium). A good first guess for the Tension of the string might be 40 N, halfway between the 50 N needed to support the large mass and the 30 N needed to support the smaller mass. At a more sophisticated level, one might guess that the Tension is slightly less than 40 N since the net force on each block must be in proportion to its mass, so the Tension must be closer to 30 N. Numeric Solution–
50 — T = 5a T — 30 = 3a. Adding the equations gives: The above equation is also the form of the shortcut, system-based solution obtained by analyzing the net force on the system (= 50 — 30 N) and including the mass of the system (= 8 kg). Solving for a gives Back-substituting for T gives both of which are in agreement with our conceptual ideas listed above. Algebraic (General) Solution–The exact analysis above will yield a general solution of the following form (m2 represents the larger mass, m1 the smaller)
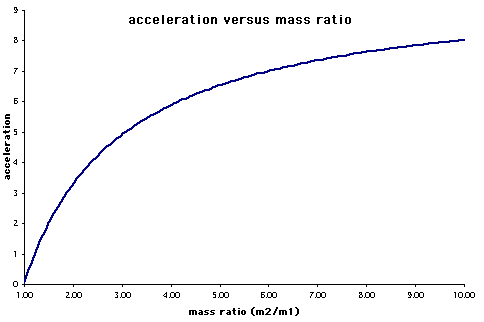
A Further, Graphical Exploration of the Atwood Problem–A method of visualizing how the value of the acceleration varies with the mass values is to graph the acceleration versus the ratio of the masses (see below). Note how the more unbalanced the masses, the closer the acceleration comes to the limiting value of g.
|
