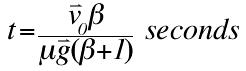| Problem: |
| A bowling ball is thrown horizontally on a horizontal lane with an initial velocity of Vo and no angular velocity. Initially, the bowling ball slides. Then it begins to roll and slide. Eventually it rolls without sliding. Solve for the time when it first begins to roll without sliding. This problem uses rotational concepts and basic calculus. |
|
Solution:
Note when torque is at a constant minimum, when the bowling ball is sliding, and when torque is at a constant maximum, when the ball is rolling. On the graph, the torque rises to its maximum after time has elapsed. However, this is an error caused by Interactive Physics, the program we used to simulate this problem, which uses integration to solve. The torque should instantaneously rise from its minimum to its maximum. The angular and linear velocities of the ball are at a maximum when the ball is sliding, but decrease as it begins to roll, and reach a minimum when it is rolls without sliding. The rotational KE of the ball increases as the ball begins to roll, while the translational and total KE's drop.
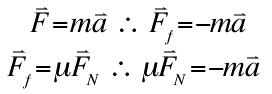
The equation above is the basic equation for force. Friction is the only force acting on the bowling ball so Ff replaces F and equals mass times acceleration. The friction force equals the friction coefficient multiplied by the normal force (mass times gravity), which therefore also equals mass times acceleration. The acceleration of the bowling ball equals its friction coefficient multiplied by gravity.
|
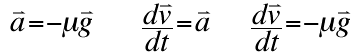
The acceleration of the bowling ball equals its friction coefficient multiplied by gravity.
Using basic calculus, we know that the derivative of velocity with respect to time equals acceleration, or the friction coefficient times gravity.
Substitute for acceleration in the second equation to find the derivative of 'v' with respect to time equal to negative friction coefficient multiplied by gravity. |
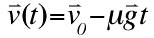
| Taking the integral of the previous equation, we find that velocity at time 't' equals a constant minus acceleration times time, or time times the friction coefficient times gravity. The constant can be found by solving the equation where time is zero and the velocity is the initial velocity. The constant equals the initial velocity. |
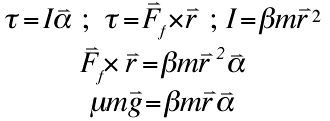
These are basic physics equations. Torque equals moment of inertia multiplied by angular acceleration. Torque also equals the forces acting on an object multiplied by the distance of this force from the point around which the force causes the object to rotate. In this case, the only force is the friction force, which is a distance r (the radius of the bowling ball) from the center of mass. The moment of inertia is defined to equal a constant multiplied by mass multiplied by the square of the radius of the object.
Set the two torque equations equal to each other and substitute for the moment of inertia to get the resulting equation above.
Substitute for the friction force and cancel the 'r's on both sides to get the third equation above. |
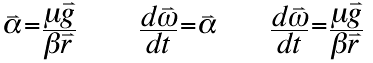
Isolating the angular acceleration symbol shows that angular acceleration equals the friction coefficient multiplied by gravity and divided by the moment of inertia constant and the radius of the bowling ball.
The above equation is another basic calculus equation. The derivative of the angular velocity with respect to time equals the angular acceleration, which therefore equals the friction coefficient multiplied by gravity and divided by the moment of inertia constant and the radius of the bowling ball. |
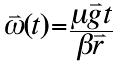
| Taking the integral of both sides of the previous equation proves that the angular velocity at time 't' equals angular acceleration multiplied by time, plus a constant. Solve the constant using initial conditions where time equals zero. At this time, since the bowling ball is sliding without rolling at all, the angular velocity is zero. The constant therefore equals zero. |
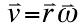
|
This is a basic rotational equation. Linear velocity equals angular velocity multiplied by angular velocity.
|
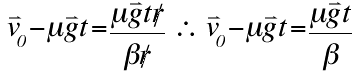
| Substitute the equation we solved to equal linear velocity and the equation we solved to equal angular velocity. Cancel the 'r's. The initial linear velocity, minus the friction coefficient multiplied by gravity and time, equals the coefficient friction multiplied by gravity, time, and the moment of inertia constant. |
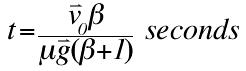
|
Time When Bowling Ball Rolls
|
| The previous equation resolves into the equation above. The time equals the initial velocity multiplied by the moment of inertia constant, divided by the friction coefficient, gravity, and one plus the moment of inertia coefficient. At this time, the bowling ball is rolling only. The angular velocity is at a maximum, while the linear velocity is at a minimum. All kinetic energy has been transferred from translational to rotational. The total KE has decreased because some energy has been lost to the friction force in the form of heat. |
|
|
Interactive Physics is a powerful simulation program that is available from MSC Working Knowledge. IP documents are playable with Interactive Physics v1.2 or later. Earlier versions may be compatible.
|
|
Text versions of the equation work are made with Microsoft Equation Editor and are embedded in Microsoft Word documents.
|
|
Movies are saved in QuickTime format available at Apple's site. Get QuickTime 4 today!
|
 |
|
|
|