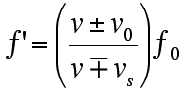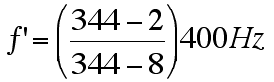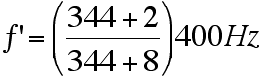| Issue: |
| When there is relative motion between the source of a sound and a listener to that sound, the pitch perceived by the listener is different from the actual pitch emitted by the source. How can we explain this phenomenon and predict its effects? |
|
Discussion:
The name of this phenomenon is the Doppler Effect, named after Christian Johann Doppler. As we all know, sound does not instantaneously travel from one point to another. It travels as a series of compression waves through a medium such as air. Doppler Theory states that if the sound source is approaching you, you will perceive the pitch as higher than it really is. If the source is moving away from you, the perceived pitch will be lower.
|
This following sound can either result from several possible situations. For example, the observer can be stationary, and the police car racing away, or the police car could be stationary, and the observer speeding away in their own car. Pay no attention to the sound getting less loud. Loudness is a completely independent effect.
|
|
Sometimes it helps to think of the Doppler Effect in terms of an analogy. Let's say you are standing several meters away from your friend on a flat surface like a parking lot. He has a bucket full of golf balls, and proceeds to roll one towards you every second. Each golf ball represents the crest of a sound wave. The ground represents the stationary medium that sound is traveling through, like air for example. He is the source; you are the listener. If you start moving towards him, (or him towards you) you will get the balls faster. If he is running away from you (or you from him!) you will get the balls at a slower rate. The faster you get the balls, the higher their "frequency." Remember that we perceive higher frequency sounds as higher pitch. Let's see if you've got the concept. Problem One: no numbers, just intuition.
 |
|
A getaway car is parked in front of a bank waiting for his accomplice inside. An off-duty officer is eating lunch in her car, which is parked far behind the robber's car. The officer notices the suspicious car. As the events progress, how does the accomplice perceive the pitch of the siren?
|
|
| 1 |
Both cars are still at rest, and Officer Parv turns on her siren
|
| 2 |
Officer Parv accelerates towards the suspicious car.
|
| 3 |
The accomplice has just gotten the car out of park, and floors it, accelerating away from the Police car.
|
| 4 |
Officer Parv also slams on her gas pedal. Her car is in great condition, so it accelerates faster than the getaway car.
|
| 5 |
The accomplice maintains his speed because he is dodging traffic, but Officer Parv can pursue him faster because he has cleared the way. Both cars travel at constant speeds, but she is gaining on him!
|
Remember that the pitch sounds higher when the Police car is closing in on the Accomplice, and lower when the distance between them is increasing. If they are accelerating towards each other, the pitch would increase with time. See a pattern? Below is the waveform of the six second chase. (Short so it won't take long to download) Superimposed on top is a graph of pitch vs. time. Play the QuickTime sound below to see if your predictions were accurate.
If something doesn't sound right to you, you should go back and reread the problem. Find your mistake. If you got it right congratulations. Moral of the story: don't run from the police! (Not that I would know anything about that) Now, let's look at something with a more mathematical foundation: How do we predict the actual perceived pitch if we know the other variables? Below is a general form of the Doppler Effect equation:
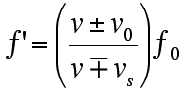
|
The f' is the perceived frequency, Vo is the velocity of the observer, Vs is the velocity of the source, V is a reference value: the speed of sound in whatever medium through which the sound is traveling. |
In this case, sound travels at 344m/s in airport air. The speed of sound through a medium is determined by an equation, factoring in the fluid medium and temperature. For now, we'll just give you 344m/s.
|
You are walking at 2m/s from your gate to the baggage claim in an airport. From behind you, one of those tram cars passes you at a brisk 8m/s. For safety reasons, it beeps at 400Hz to let people know it is coming. What pitch do you hear as it approaches you from behind? What about after it passes you? <Think about the sign convention.>
|
This is what the driver of the cart hears:
|
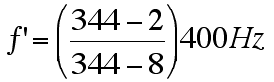
|
You (who are walking away) would make the pitch lower, so the sign in the numerator would be minus. The cart (which is moving towards you) is effectively raising the pitch. To make the result larger, we need to make the denominator smaller, so the sign would again be minus. |
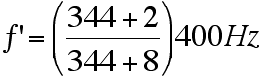
|
Once the cart passes you, things are reversed. |
|
The first pitch would be a little over 407Hz, while the second comes out to about 393Hz. Always, always, always, look at your numerical answers and see if they make sense with your predictions. If the source and observer are speeding towards each other, it wouldn't make any sense to have a lower perceived pitch!
|
This is what you hear. (After two beeps, the cart passes you!)
|
|
|
All graphs made with Graphing Calculator, which is included with any Macintosh System Software package since MacOS 8.
|
|
Text versions of the equation work are made with Microsoft Equation Editor and are embedded in Microsoft Word documents.
|
|
Movies & Sounds are saved in QuickTime format available at Apple's site. Get QuickTime 4 today!
|
 |
|
|
|